3.1.1 Introducción |
 |
Hasta ahora hemos estudiado curvas
en un plano descritas mediante una ecuación cartesiana. Es
decir, hasta ahora, los puntos de una curva han estado especificados por
una ecuación en coordenadas rectangulares.
Esta no es la única forma de
especificar una curva en un plano. En este cuaderno estudiaremos otra forma
de describir una curva en el plano, mediante un par de ecuaciones, llamadas ecuaciones paramétricas.
A manera de introducción, repasaremos el movimiento de un proyectil.
Movimiento de un proyectil
El movimiento de una partícula a lo largo de una curva
se llama movimiento curvilíneo.
En física se demuestra que
el movimiento de un proyectil ocurre en un plano, digamos el plano xy,
y que dicho movimiento está regido por el hecho de que su aceleración
en las direcciones x, y satisface las condiciones
| ax = 0, ay = - g, |
en donde g es la aceleración de la gravedad, y por definición de aceleración,
| ax = x´´(t), ay = y´´(t). |
En t = 0 se toma x = xo, y = yo y las componentes de la velocidad inicial vo son
vox = vo Cos(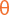 )
, )
, |
voy = vo Sen(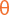 ) ) |
Observa la siguiente figura.
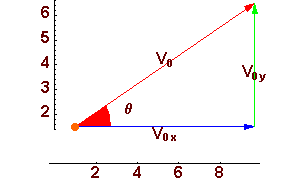 |
vo = 10 m/s
ángulo 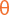 = = 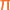 /6 /6 |
vox = 10
cos (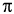 /6)
= 5(3)1/2 /6)
= 5(3)1/2 voy = 10 sen ( 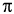 /6)
= 5 /6)
= 5 |
Integrando las ecuaciones de las componentes de la aceleración con respecto al tiempo, obtenemos las componentes de la velocidad en las direcciones x, y.
| ax = 0; | ay = -9.8; | |||||||
 |
t | |||||||
| vx - vox | = | o | ax dt | = | 0 |  |
vx = vox | |
 |
t | |||||||
| vy - voy | = | o | ay dt | = | -9.8 t |  |
vy = voy - 9.8 t | |
Integrando estas con respecto al tiempo, obtenemos las componentes de la posición.
| x = xo + vox t, | |||||
| y = yo +voy t - |
|
g t2 |
En estas últimas ecuaciones, las coordenadas (x, y) de la
partícula dependen de un parámetro,
que es el tiempo t.
A ecuaciones de este tipo se les llama ecuaciones paramétricas y describen
el movimiento de la partícula en un intervalo 0
<= t <= T.
En el presente ejemplo, T es el tiempo en el que la partícula choca contra el suelo.
Observa el movimiento de la partícula,
dadas las condiciones iniciales xo = 1, yo = 1.5, vo = 10 y el ángulo 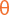 = 30°.
= 30°.
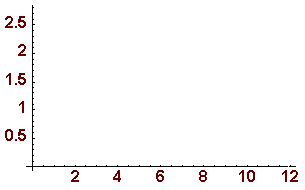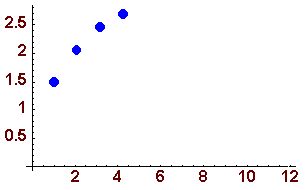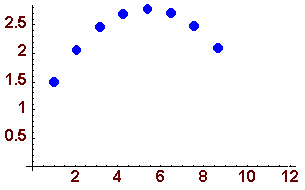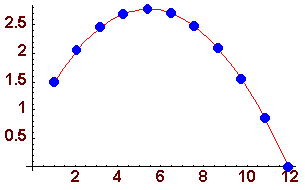 |
x(t) = 1 + 5(3)1/2t y(t) = 1.5 + 5t - 4.9t2 |
Como pudimos observar, las ecuaciones paramétricas dadas describen la trayectoria de la partícula, que en este caso es una parábola.


